Закон Бернулли

История

Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли^{[K 1]}. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году^[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости — Эйлером в 1757 году^[12].

Интеграл Бернулли в несжимаемой жидкости

Полное давление
Размерность
Единицы измерения
СИ	Дж/м³ = Па
СГС	эрг/см³
Примечания
Постоянно вдоль линии тока стационарного течения несжимаемой жидкости.

Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина сохраняет постоянное значение вдоль линии тока:

Здесь

— плотность жидкости;

— скорость потока;

— высота;

— давление;

— ускорение свободного падения.

Элементарный вывод уравнения Бернулли из закона сохранения энергии[показать]

Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением^[2]. Могут также использоваться термины «весовое давление» , «статическое давление» и «динамическое давление» . По словам Д. В. Сивухина^[13], нерациональность этих понятий отмечалась многими физиками.

Размерность всех слагаемых — единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии^[14]).

Вывод формулы Торричелли из закона Бернулли

Основная статья: Формула Торричелли

Иллюстрация формулы Торричелли

В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:

где

— высота столба жидкости в сосуде, отсчитанная от уровня отверстия,

— скорость истечения жидкости,

— атмосферное давление.

Отсюда: . Это — формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты . Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде^[15].

Другие проявления и применения закона Бернулли

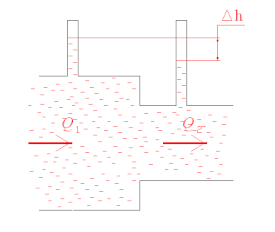
Закон Бернулли объясняет эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем в широкой части

Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука^[16].

Основная статья: Эффект Вентури

Вдоль горизонтальной трубы координата постоянна и уравнение Бернулли принимает вид . Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури^[17] и струйного насоса^[1].

Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)^[18].

Применение в гидравлике

Основные статьи: Гидравлика, Гидравлические потери и Напор

Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» :

где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:

Напор^[19]
Размерность
Единицы измерения
СИ	метр
Примечания
Полное давление, делённое на удельный вес.

— гидравлическая высота^[4] или напор^[19],

— нивелирная высота^[4],

— пьезометрическая высота^[4] или (в сумме с нивелирной высотой) гидростатический напор^[19],

— скоростная высота^[4] или скоростной напор^[19].

Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»^[19].

Интеграл Бернулли в баротропных течениях

Основная статья: Баротропность

Уравнение Бернулли может быть выведено и из уравнения движения жидкости^{[K 2]}^{[K 3]}. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: , что позволяет ввести функцию давления^[22] В этих предположениях величина

постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом заменяется на потенциал массовой силы .

Вывод интеграла Бернулли для баротропного течения[показать]

Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости , интеграл Бернулли в виде ^{[K 4]} сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения^[25].

Формула Сен-Венана — Ванцеля

Если в течении совершенного газа выполняется адиабатический закон^[26]

то уравнение Бернулли выражается так^[27] (вкладом от силы тяжести обычно можно пренебречь):

вдоль линии тока или вихревой линии. Здесь

— показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме,

— давление и плотность газа,

— условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.

С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за тогда скорость истечения выражается через внешнее давление по формуле Сен-Венана — Ванцеля

926 19.03.2021